曲面铣削过程加工路径对切削力和磨损的影响研究

在球头铣刀铣削难加工材料Cr12MoV过程中，由于刀尖处切削速度为零，曲面形状呈不规则变化，因此大部分切削均发生在切削侧刃上，从而导致刀具与工件的摩擦和犁削。为了减小由于加工参数选取不准确引起的振动和刀具磨损，进而提高刀具寿命和工件质量，对不同路径加工复杂曲面过程中刀具与工件接触部分的未变形切屑厚度进行研究，并优选铣削参数。

为了获得加工参数和几何参数对切削力的影响规律，国内外学者在切削力模型的研究方面进行了许多工作。K.Nakayama等基于多铣削参数建立了立铣刀铣削刃微元铣削力模型，但该模型并未考虑切削速度的影响。冯志勇等利用几何知识和收敛效率，建立了考虑切削过程中的刀具几何参数关系的铣削力模型。X.Zhang等研究了复杂曲面铣削过程中的刀具切入角与切出角，建立了一种外圆铣削加工中铣削力的预测模型，相较于传统铣削力预测模型，预测精度得到增强。J.W.Ma等基于加工表面的几何特征建立了一种新型铣削力模型，可以预测不同主轴转速下变切削速度的铣削力波动趋势，为复杂曲面加工过程中的参数优化提供了理论基础。郝洪艳等通过计算刀具和工件的切入角和切出角，建立了一种凸凹曲面周铣铣削力预测模型，在此基础上分析了曲率对铣削力的影响，结果表明，曲率对凹曲面铣削的影响较凸曲面更加显著。

切削加工过程中的刀具磨损是检验刀具使用性能最直接的方式，刀具的磨损值在不同程度上反映了工件的加工性能，合理控制球头铣刀铣削过程中的刀具磨损量有助于优化铣削加工工艺参数。B.Sun等进行了球头铣削刀具磨损试验，根据试验结果建立铣削刃径向磨损模型，然后建立以最大效率和最小成本为目标的铣削工艺优化模型。试验结果表明，该模型具有较高的精度，可用于预测磨损量。冯闯研究了球头铣刀铣削高温合金过程中不同刀具的磨损机制，建立了加工复杂曲面的球头铣刀刀具磨损预测模型，可以达到精准的预测效果。岳彩旭等采用PCBN刀具进行铣削Cr12MoV模具钢磨损试验，分析了切削速度和进给量对刀具磨损的影响，为提高加工效率、提升刀具寿命的研究提供了理论支持。

目前研究主要集中在单一加工方式下的铣削参数优化和表面几何特征对铣削力和磨损的影响，对于不同切削路径加工复杂曲面难加工材料的切削力、刀具磨损影响规律的研究较少。本研究的目的是通过计算不同切削路径下的球头铣刀与曲面零件之间的未变形切屑厚度的瞬时变化，分析相同切削面积条件下的铣削力变化规律；在此基础上，基于不同切削参数对刀具磨损的影响，使用线性回归分析方法建立不同切削路径的刀具磨损预测模型，并进行验证。

1 试验设计

采用大连机床厂生产的VDL-1000E型三轴立式加工中心数控铣床进行试验；工件材料为Cr12MoV；测力仪器选用Kistler 9257B测力仪；采用基恩士KEYENCEVHX-1000型超景深显微镜进行磨损值检测；刀具选用厦门金鹭的整体硬质合金球头铣刀，型号为SH260-B2-6-9-H，球头铣刀的直径Φ6mm，球头铣削刀刃为2刃，试验加工现场和加工用刀具见图1，铣削过程中不使用铣削液。

 (a)试验加工现场(b)两刃球头铣刀

图1 加工现场和球头铣刀

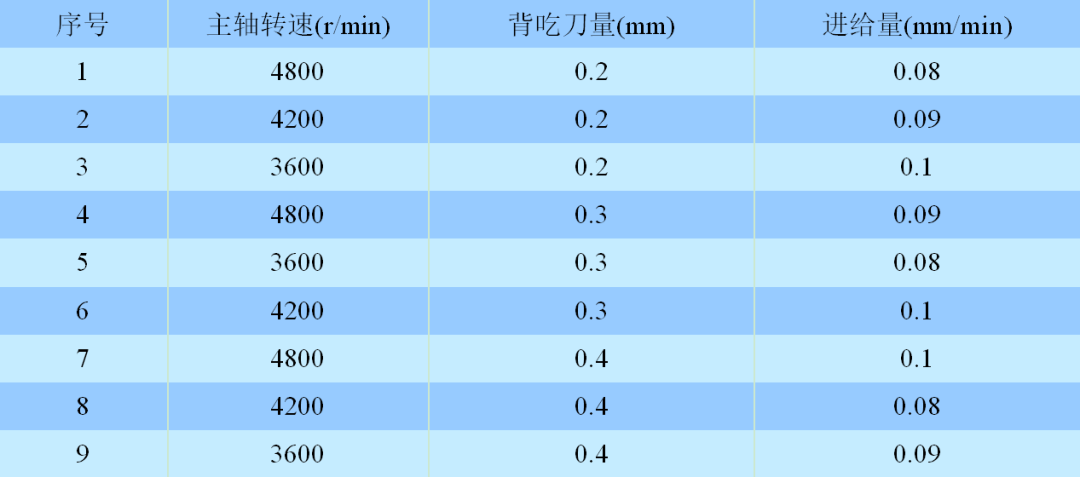
在刀具逐渐磨损的过程中，通过往复走刀、环形走刀的两种不同走刀路径进行铣削力和刀具磨损值的测量，采用的正交试验参数见表1。

图2为两种走刀路径的示意图，圆圈代表起始走刀位置，箭头方向代表进给方向，往复走刀每一回合分为顺铣和逆铣两种加工方式，环形走刀路径只存在顺铣的加工方式。

表1 正交试验因素表

 

为了减少外界因素对试验结果的影响，往复走刀和环形走刀均采用新刀进行加工，加工去除相同的材料量后，设计停机程序，通过超景深显微镜测量后刀面磨损值。往复走刀和环形走刀在每次加工过程中分别测得3组和5组铣削力信号，通过数据采集卡获得放大后的切削力信息，并传输到电脑上。为了提高加工效率，减少空走刀和空切削的情况，程序设计两种走刀路径下的刀具和工件始终保持相互接触。  

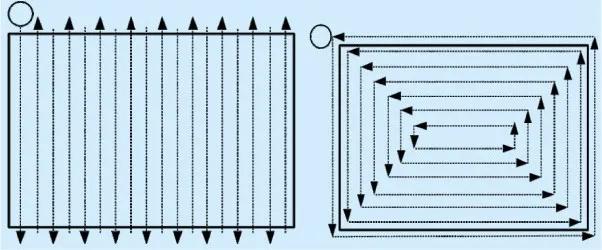
(a)往复走刀     (b)环形走刀

图2 两种走刀路径

2 铣削力分析

在不同走刀路径下切削同一层材料的过程中，通过三相测力仪测量X，Y，Z三个方向的切削力滤波信号如图3所示，由于加工过程中存在切削振动，试验存在一部分小幅未知的噪声信号。切削力信号的变化是由于未变形切屑厚度引起，在进给过程中，刀具转一圈，切削刃参与切削的面积随时间变化可以在一个周期内观察到两个峰值，这是由于两个削刃连续切削的结果。

针对一个工序的往复走刀单周期信号如图4所示。往复走刀过程中，两条临界线1，7之间为一个加工周期，其中图4a中1-3与4-6为往复走刀的曲面切削过程，代表图4b中切削的曲线路径；图4a中3-4，6-7为拐角后的直线切削过程，代表图4b中切削的直线路径。

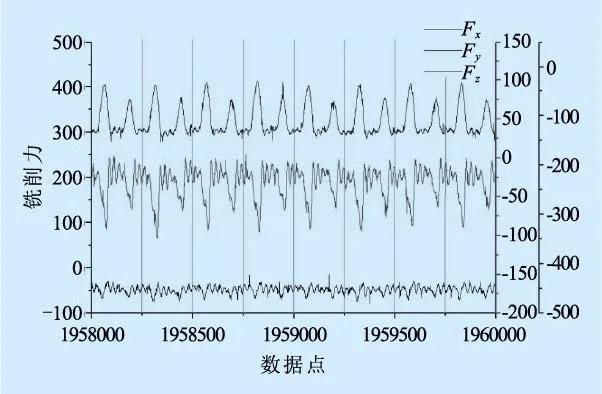
(a)往复走刀铣削力

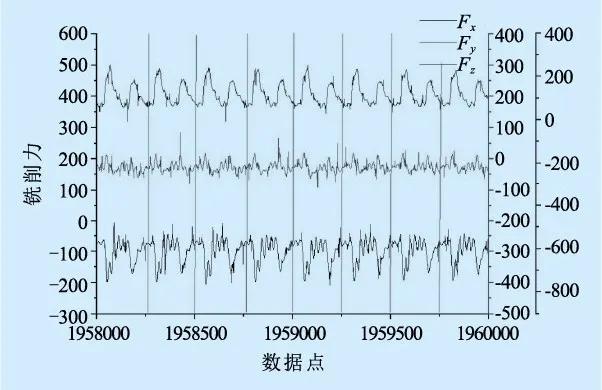
(b)环形走刀铣削力

图3 两种走刀路径铣削力信号

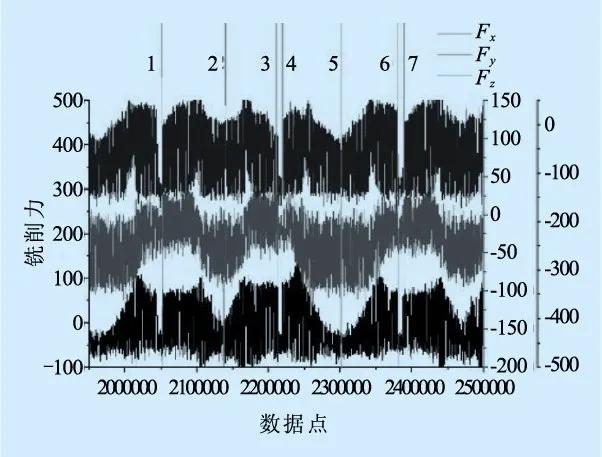
(a)铣削力信号

(b)加工工件

图4 往复走刀单周期信号

针对一个工序的环形走刀单周期信号如图5所示。环形走刀过程中两条临界线1，6之间为一个加工周期，其中图5a中3-4与5-6为环形走刀的直线切削过程，代表图5b中切削的直线路径；图5a中2-3与4-5为环形走刀的曲面切削过程，代表图5b中切削的曲线路径；1-2为由外环铣削向内环铣削的进给过程。由图可以看出，环形走刀过程中，直线切削的铣削力变化平缓且略大于曲面切削的铣削力，这是由于平面切削过程参与切削的接触面积呈现周期性变化；而在曲面切削的过程中，由于曲面存在曲率，刀具与工件的接触过程可以看作是切削刃的侧刃接触切削的过程，在凹凸表面铣削是X，Y方向上铣削的变化较为显著，并且铣削力的增大也会加剧刀具的磨损程度。

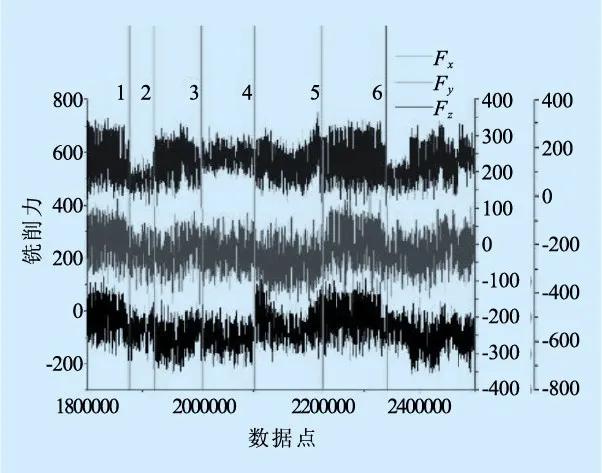
(a)铣削力信号

(b)加工工件

图5 环形走刀单周期信号

曲面铣削过程中的工件形状不规则，刀具进给方向随着加工路径不断改变，主要体现在两个连续切面之间的未变形切屑厚度和切削力的变化上。对球头铣刀加工复杂曲面时的未变形切屑厚度进行几何建模，将球头铣刀切削刃沿等径向角度间隔分层离散成有限个很小的切削微元，其微元层如图6所示。在接下来的研究中，假定切削过程中没有出现刀具跳动、刀具偏心和刀具弹性挠动，其中斜线区域为切削接触面积。

图6 曲面铣削微元层

由图6可以看出，阴影部分为铣削过程中的接触区，建立以前一刀球心O为原点的刀具坐标系，其中，刀具半径为R，两刀球心之间距离OM为进给量fz，切削深度为ap。其中，已加工表面的圆弧半径为R1；待加工表面的圆弧半径为R2=R1+ap；ξ为曲面铣削的过程角度，ξ=nα，α为每齿转向角，n为可加工的齿数。

根据图中几何关系可得

 

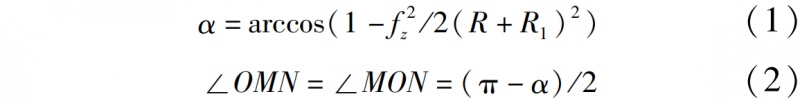
接触区域中黑色部分为刀具切削刃对于Z轴的位置角φ时的某个切削微元。

对于曲面铣削过程，在△OMQ中有

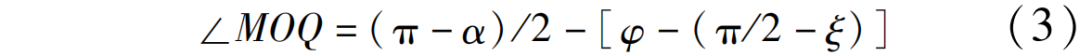
图7为直线铣削过程中的接触区，在△OMQ中有

 

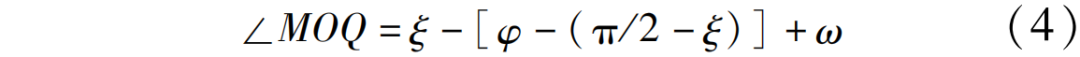
式中，ω=π/2-ξ。

根据三角形余弦定理可得

 

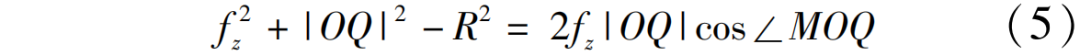
结合上述条件，在位置角φ时的最大未变形切屑厚度可以表示为

 

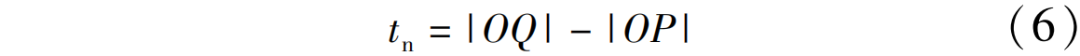
当φ>π/2时，|OP|=R/cos(φ-π/2)；当φ≤π/2时，|OP|=R。

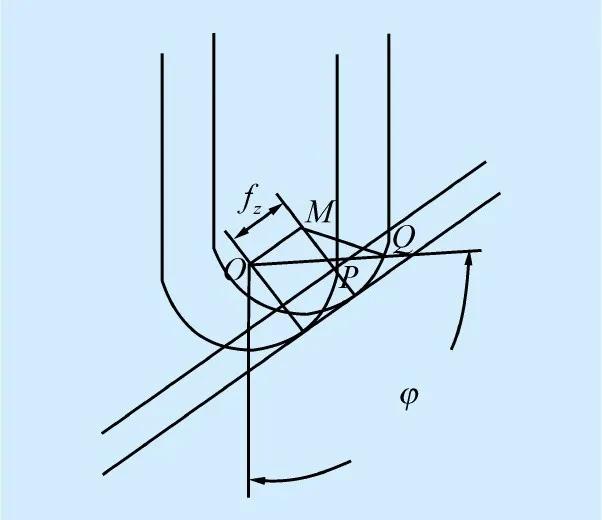
图7 直线铣削

曲面铣削过程中的∠MOQ略大于直线铣削过程中的∠MOQ，不同的未变形切屑厚度的变化差异直接影响切削力的大小，采用MATLAB软件计算出在同参数条件下直线加工与凹凸曲面加工过程的最大未变形切屑厚度的差值如图8所示。可见，在相同条件下，直线走刀比凹凸曲面加工的最大未变形切屑厚度tn大很多，所以直线走刀的切削力略大于凹凸曲面加工的切削力。

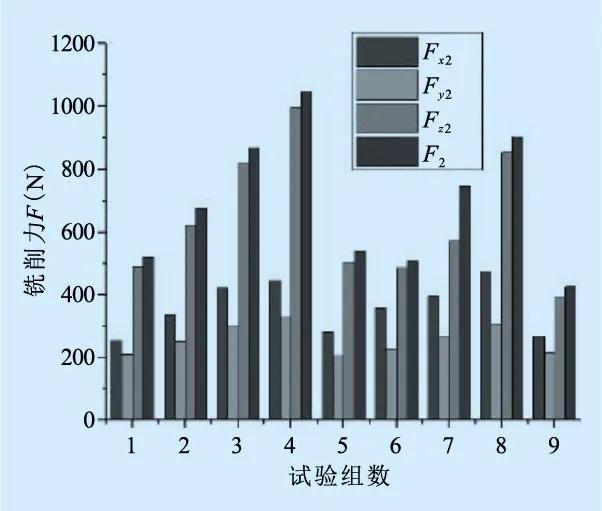
在实际加工过程中，较多注重铣削力的极值问题，为降低通过压电片三向测力仪采集到的铣削力信号冗余数据的影响，采取Origin软件取切削周期中的极大值进行差异化研究得到有效数据。铣削合力为三个铣削分量Fx，Fy和Fz的矢量和，往复铣刀和环形铣刀的铣削力结果见图9。

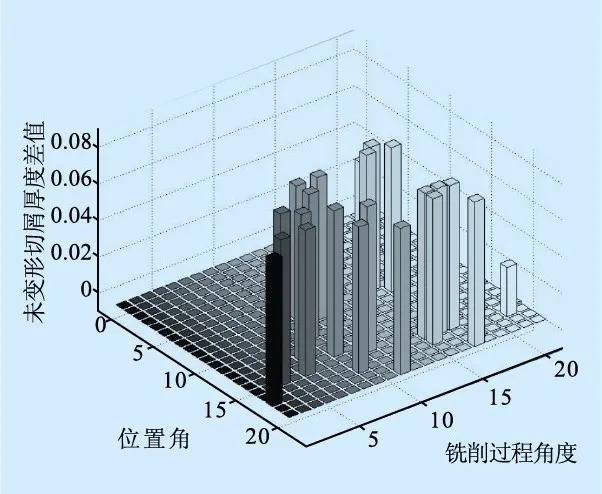
图8 未变形切屑厚度差值

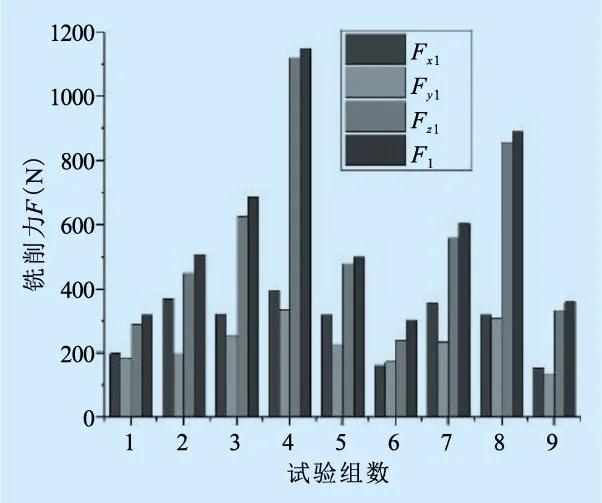
(a)往复走刀

(b)环形走刀

图9 两种走刀路径下的铣削力变化

往复走刀和环形走刀在铣削相同铣削层时的材料去除量相同，而两种走刀路径下刀具与工件始终保持相互接触，通过计算得出球头铣刀所铣削长度分别为L1=32803mm和L2=32683mm，往复走刀路径的材料去除率略小于环形走刀的材料去除率，因此环形走刀路径测得的切削力普遍大于往复走刀测得的切削力。

3 磨损分析及建立磨损预测模型

（1）磨损分析

采用比极差法更简单的方差分析法分析不同走刀路径下主轴转速、背吃刀量和进给量对刀具磨损的影响规律，并计算出各因素对其影响的显著程度。

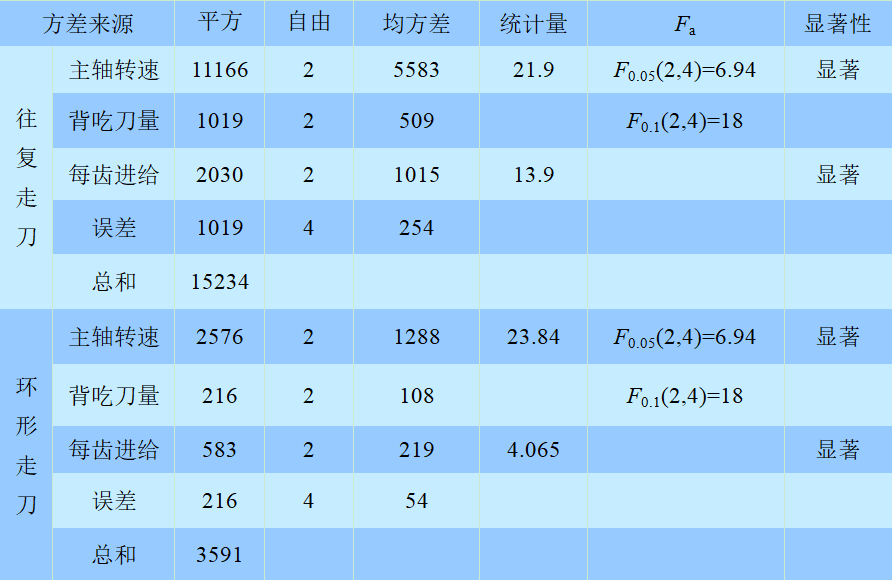
表2为两种不同的走刀路径下刀具磨损的方差分析表。通过计算各因素的平方和、自由度、均方差和统计量可以看出，在往复走刀路径下，对磨损影响最大的因素是主轴转速，其次是每齿进给量，影响最小的是背吃刀量；在环形走刀路径下，对磨损影响最大的因素是每齿进给量，其次是主轴转速，影响最小的是背吃刀量。

表2 磨损量VB的方差分析表

 

（2）建立磨损预测模型

采用多元线性回归的方法建立刀具磨损预测模型，通过仿真计算出不同走刀路径的铣削长度，分析复杂曲面的几何形状变化。球头铣刀铣削曲面时，球头铣刀有效切削半径和未变形切屑厚度随时发生变化。为了精准预测球头铣刀磨损，在建立磨损模型的过程中需要考虑不同切削参数对磨损的影响，同时需要引入相关系数来减少机床振动或其他外界条件对刀具磨损的影响，得到修正的刀具磨损公式可表示为

 

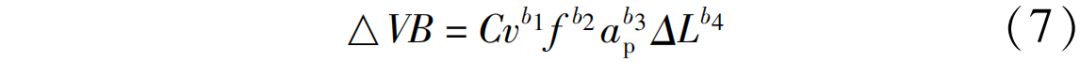
式中，v，f，ap，△L分别表示铣削速度、进给速度、铣削深度、刀具磨损检测时的铣削长度；b1，b2，b3，b4分别是对铣削速度、进给量、铣削深度、铣削长度的影响指数，对影响刀具磨损变量所选定的系数进行修正。C表示相关系数，影响因素为刀具和工件材料的性能。

为了确定该预测模型的系数，通过正交试验测得刀具磨损量值，利用最小二乘法原理，可得到多元线性方程组参数的最小二乘估计矩阵为

 

 

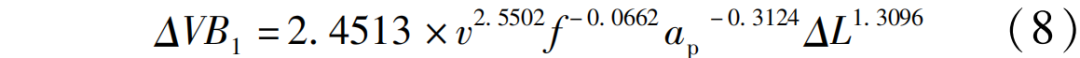
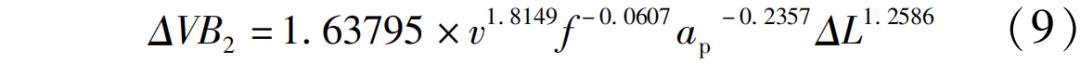
式中，△VB1、△VB2分别表示往复走刀、环形走刀的刀具磨损值。

为了验证不同走刀路径的刀具磨损预测模型是否准确，需要计算均方、统计量、P以及总体自由度等数据，对刀具磨损的线性回归方程进行显著性水平检验。

表3为不同走刀路径下磨损量VB的显著性检测结果。表中数据量为6，自变量为4个。

表3 磨损量VB显著性检测

 

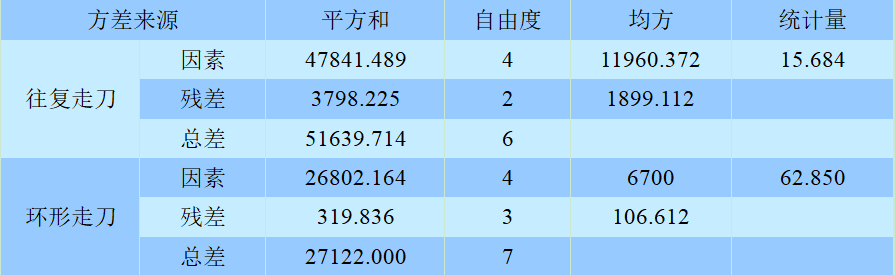
通过经验查询显著性水平为0.05。从表3可以看出，往复走刀和环形走刀的统计量数值分别为15.684和62.850，而计算得F(m，n-m-1)=F 0.95 (4，4)=6.388，同时P值低于所设定的显著性水平。从数据可以看出，上述预测值和试验值的线性关系良好，表明球头铣刀铣削曲面的刀具磨损的预测值与实际加工值相吻合（见图10）。

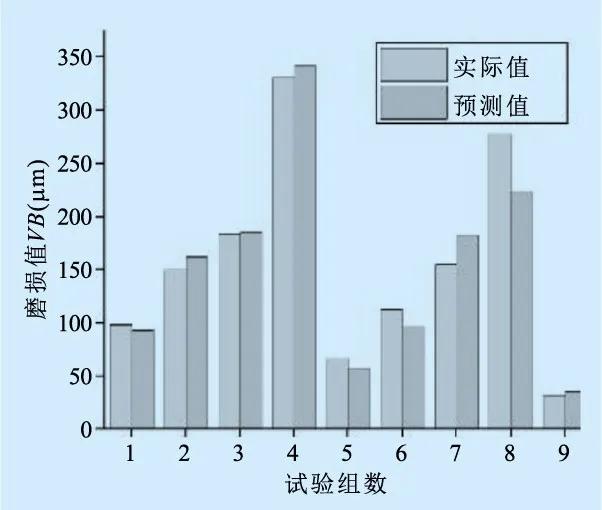
(a)往复走刀

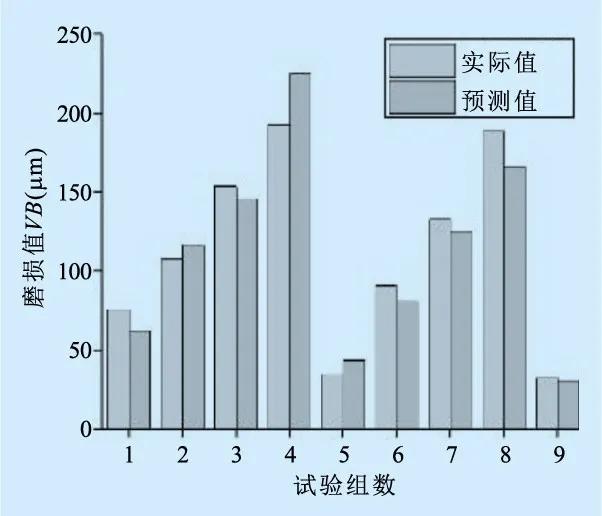
(b)环形走刀

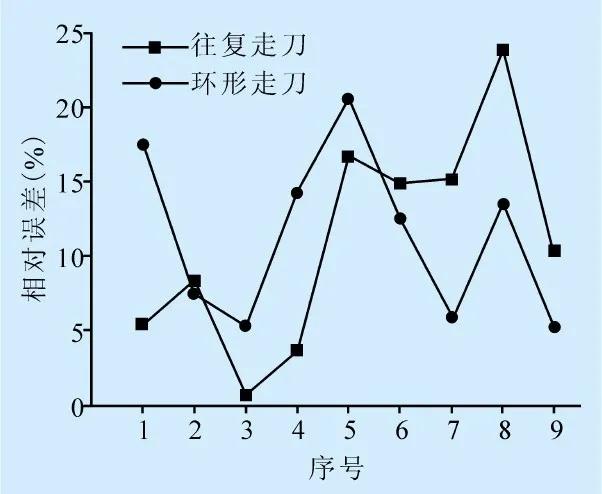
(c)相对误差值

图10 刀具磨损的试验值与预测值对比

通过对球头铣刀铣削曲面的不同走刀路径下刀具磨损试验获得的实际值与根据刀具磨损预测模型获得的预测值进行对比分析，基本的预测误差不超过23%，验证了不同走刀路径下刀具磨损预测值的准确性。

小结

建立了直线与曲面切削过程微元模型，通过对比分析直线铣削和曲面铣削过程中的最大未变形切屑厚度，直线走刀的最大未变形切屑厚度大于凹凸曲面，因此单周期内的直线走刀的切削力略大于凹凸曲面加工的切削力。通过试验与理论研究分析，相同材料去除量的条件下，往复走刀路径的材料去除率略小于环形走刀路径的材料去除率，因此，铣削相同铣削层时，环形走刀路径测得的切削力普遍大于往复走刀路径测得的切削力。运用方差分析法分析了不同走刀路径下各铣削参数对刀具磨损影响的显著程度，并通过多元线性回归的方法得出不同走刀路径下刀具磨损预测模型，运用F检测出高度显著性，得出该模型的预测误差在23%之内，验证了其准确性。