基于切屑尺寸控制的缸盖面铣工艺优化

水套是冷却液循环流动的通道，主要对发动机燃烧室进行冷却，结构较复杂。图1为用三维软件逆向生成的某型号发动机水套三维模型。当对缸盖进行面铣加工时，部分切屑残留在水套中，导致后续清洗工艺难以有效将发动机切屑清洗带走，残留切屑将会对发动机性能造成安全隐患。

图1 某型号发动机水套

图2为某次清洗试验后水套内部的残留切屑。试验中，缸盖采用线切割切成三段，用螺栓连接紧固，将切屑从外部塞入水套孔中进行清洗试验，之后松开螺栓，查看水套内部切屑残留情况。

Batzer S.A.等通过钻削铸造铝合金试验指出，钻削材料、进给量和钻头结构对切屑大小有较大影响；Davis B.等通过镁基复合材料车削试验指出，切削速度较小时（<0.5m/s），切屑以锯齿状为主；切削速度较大时，切屑以颗粒状为主；Wanger W.等研究了切削参数、刀具结构和冷却条件对切屑形貌的影响，以控制切屑的厚度、长度和密度等，使切屑便于回收利用。可见，通过优化加工参数和主动控制切屑的形状和尺寸使后续清洗工艺能够有效带走残留切屑，对于发动机质量的稳定性和生产线运行过程的可靠性具有重要意义。

图2 水套卡屑

本文基于缸盖面铣切削试验获得不同参数下的切屑形貌和尺寸，求取其平均切屑厚度、宽度和卷曲半径后进行回归分析，求得不同参数下切屑尺寸的拟合公式。进而通过理想的切屑尺寸，反求合理的加工参数区间，有利于后续清洗工艺带走残留在水套中的切屑。

1 试验方案与设计

（1）试验过程

以发动机缸盖为加工对象进行精铣加工。加工材料为ZAlSi11Cu2（ZL113）硅铝合金，由于其质量轻、综合力学性能好，符合节能减排的需求，被广泛应用于汽车产业。试验所用刀具为MAPAL的PCD刀具，直径125mm，共有10个齿。所有试验均为干式切削，采用基恩士VHX-600超景深显微镜测量切屑尺寸。为保证样本的准确性，每组参数测量10个切屑，分别测量其厚度、宽度和卷曲半径，然后求取其平均值。表1为试验所用加工参数，表2为试验结果。

表1 试验加工参数

表2 试验结果

（2）回归模型

采用幂函数形式对切屑尺寸进行拟合，可得

式中，a为切屑厚度；b为切屑宽度；r为切屑卷曲半径；v为切削速度；f为进给量；li、mi、ni为系数，i=1、2、3。

为保证拟合精度，精铣切屑尺寸线性回归时做以下两点假设：

①铣削时切屑多具有多个卷曲半径，回归取其最大值。

②为保证回归分析结果的准确性，所选切屑尺寸为各组参数中出现频率较高的切屑，个别形状不规则或较少量的切屑不在回归分析之内。因为不同切屑变形程度不同，其宽度、厚度和卷曲半径也有较大差别，为保证拟合精度，只选取常见切屑进行拟合。图3为精铣发动机缸盖时的切屑形貌，螺旋状切屑较多，故切屑尺寸拟合以螺旋状切屑为主。

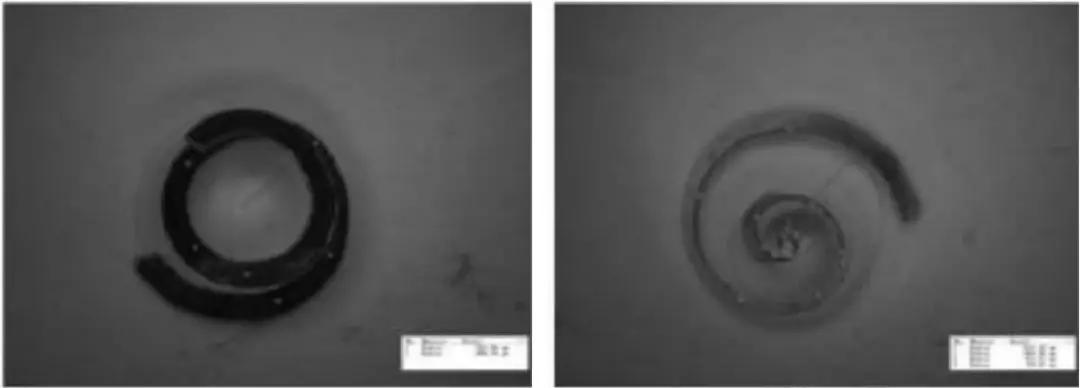
(a)短锥度螺旋状切屑（少量）（b）螺旋状切屑（大量）

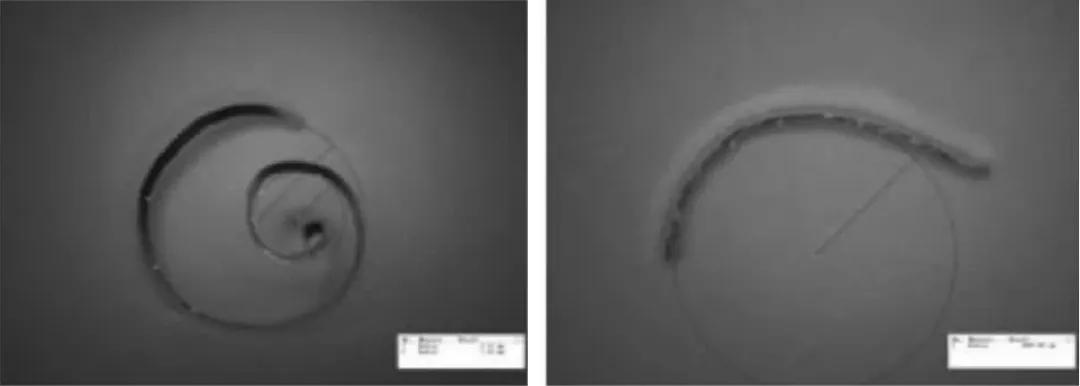
(c)螺旋状切屑（大量）（d）圆弧切屑（少量）

图3 切屑形貌

对式（1）、式（2）和式（3）两边取对数，得到线性方程为

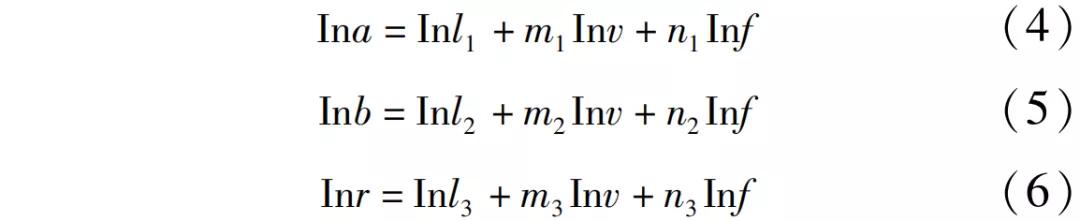
将Inli视为新的未知数Li，通过对切屑平均宽度、厚度、卷曲半径以及切削速度和进给量取自然对数进行多元线性回归，即可求得系数li、mi和ni（i=1，2，3）。

2 试验结果分析

（1）回归模型有效性分析

通过取自然对数可以将切削速度、进给量与切屑尺寸转化为线性关系进行线性回归，可以求得式（1）、式（2）和式（3）中的系数，从而建立切削参数和切屑尺寸间的经验公式。回归公式为

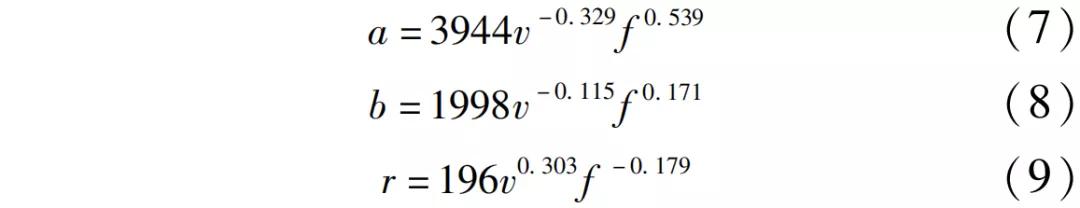
对式（7）、式（8）和式（9）进行方差分析，对回归模型的有效性进行检验，判断其显著性。设α=0.05，回归模型有效性分析见图4。查F分布表得F0.05（2，9）=3.01，由于各回归模型F值均大于3.01，故回归模型有效。

图4 回归模型有效性分析

（2）切削参数对切屑尺寸的影响

切屑厚度是与每齿进给量相关的参数，在理想情况下，切屑厚度的值等于fsinκr(κr为刀具主偏角，见图5)。但由于切削过程中切屑受挤压会发生变形，通常切屑厚度大于切削层厚度。

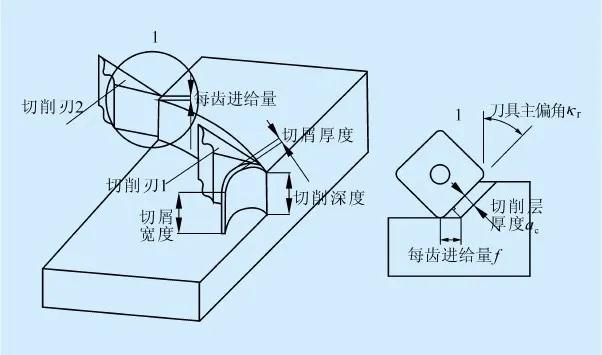
图5 切屑尺寸与切削参数的关系

图6为切屑厚度随加工参数的变化情况。由图可见，切屑厚度随进给量的增加而增加，随转速的提高而减少。这是由于切削速度越大，金属流动速度大于塑性变形速度，终始滑移线OM后移，剪切角 增大。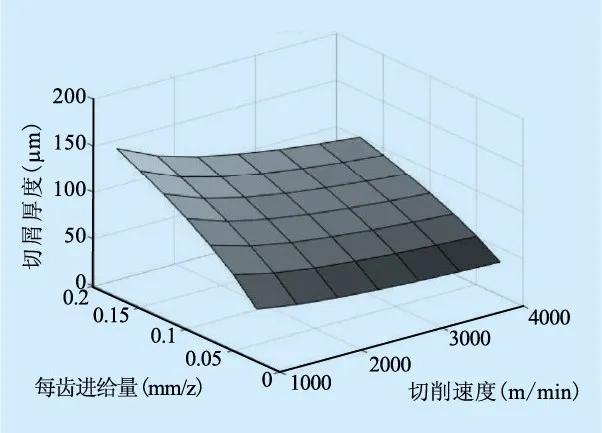

 

图6 切屑厚度与切削参数的关系

剪切角 与变形系数ξ的关系为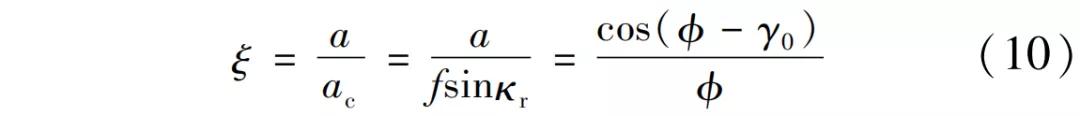

 

式中，ac为切削层厚度；γ0为前角。

由式（10）可知，当剪切角增大时，变形系数减小，切屑厚度也减小；当切削速度增加，摩擦系数减小，因此变形系数减小，切屑厚度也随之减小。

图7为切屑宽度随切削参数的变化情况。由图可知，在理想情况下，切屑宽度值等于切削深度值。切屑宽度随切削参数的变化趋势与切屑厚度一致，即随切削速度的增加而减小，随进给量的增大而增大。

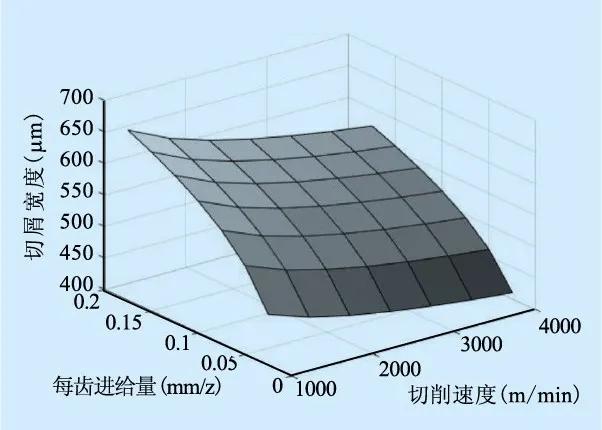
图7 切屑宽度与切削参数的关系

切屑宽度和切屑卷曲半径是影响发动机缸盖切屑清洗去除效果的两个重要参数。图8为某次清洗试验结束后、缸盖内部切屑的残留情况。由图可以看出，切屑大多卡在水套槽中，难以有效排出。

图8 清洗试验结果

除清洗工艺的优化外，切屑尺寸本身的控制（切屑宽度、卷曲半径）也是优化清洗效果的重要方法。

图9为切屑卷曲半径随切削参数的变化关系。由图可见，切屑卷曲半径随切削速度的增大而增大，随进给量的增大而减小。这是由于随切削速度的增加，刀—屑接触长度比λ减小，切屑卷曲半径增大。故有效降低切削区域温度，可以有效降低切屑卷曲半径和切屑尺寸，使切屑更容易被清洗带走。此外，随着进给量的增大，切削厚度和应变增大，从而易于断屑，切屑卷曲半径减小。

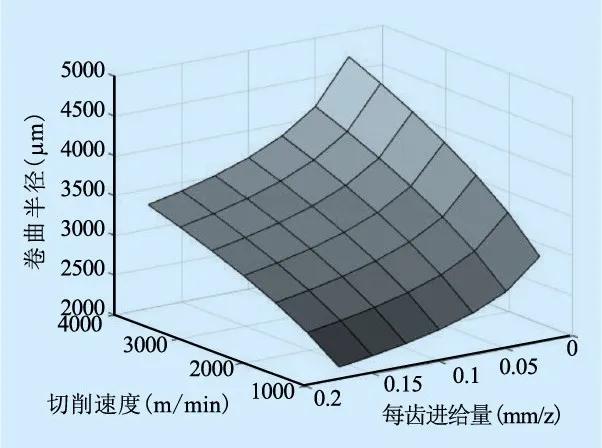
图9 切屑卷曲半径与切削参数的关系

3 基于等高线图的切削参数优化

收集并测量清洗试验结束后水套内残留切屑的宽度和卷曲半径，发现残留切屑的卷曲半径多数大于3600μm，而宽度多数在520μm以上。考虑到生产节拍，零件加工效率应保持在一定区间内。材料去除率Q可定义为

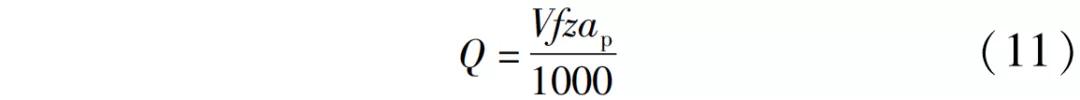
式中，z为面铣刀齿数。

需要指出的是，精铣加工时的切削深度为定值0.5mm，故影响材料去除率的因素只有切削速度和每齿进给量两个变量。将材料去除率拟定为0.6~0.8cm3/min。

图10为切屑宽度、卷曲半径和材料去除率的等高线图，图中实线为材料去除率等高线，虚线为切屑卷曲半径等高线，点画线为切屑宽度等高线。根据以上限定条件，可知精铣加工参数范围为图中斜划线区域。

图10 切屑宽度、卷曲半径和材料去除率等高线

小结

(1)建立了切削参数和切屑尺寸之间的回归模型，并通过数理统计分析证明了回归模型的合理性。

(2)试验发现切屑厚度和切屑宽度随切削速度的增大而减小，随进给量的增大而增大；切屑卷曲半径则与之相反，随切削速度的增大而增大，随进给量的增大而减小。

(3)根据清洗试验残留切屑宽度和卷曲半径的尺寸，并将材料去除率考虑在内，根据等高线图可以优化出适于切屑清洗的面铣加工参数。