基于达索系统SIMULIA Isight的汽车扭转梁参数化设计方法

许诺，曹露芬，李华斌，翁洋，王光耀，孙成智

上海汽车集团股份有限公司乘用车技术中心
 

摘要：本文提出基于Isight的参数化设计方法，优化得到的扭转梁满足操稳性能和耐久性能的要求，同时方案具备较好的轻量化意义。利用Isight软件，集成SFE、Nastran、ncode、Abaqus，完成刚度、耐久及强度多目标自动化优化，缩短了90%的优化周期。
 

关键字：扭转梁；参数化；多目标自动化优化
 

0 前言

当前，汽车行业竞争愈发激烈，如何缩短汽车产品的设计周期，提高设计效率，成为所有汽车企业研究的重点[1]。王平等[2]运用多目标遗传算法结合多学科协同优化对车身吸能部件板厚及车门屈服应力作为变量，进行多目标优化设计；李锦等[3]基于灵敏度分析方法，以副车架部件厚度作为优化变量，进行强度和模态多目标优化；蒋荣超等[4]基于网格变形技术，对开口梁进行了形状变量和厚度变量设计，以质量、疲劳、刚度为优化目标进行了优化设计。而对于结构较复杂的汽车扭转梁结构，国内外关于其选型及形状参数化设计的研究则少见报道[1-5]。

扭转刚度是扭转梁重要的固有性能之一，决定了扭转梁在轮心反向跳动时抗扭转能力。反映到整车车辆特性上，扭转梁自身的扭转可以有效降低车身侧倾，扭转刚度越大，对车身侧倾减小程度越大；但是扭转刚度过大，会影响整车平顺性。在不同车型开发过程中，整车操稳性能要求的侧倾刚度随轴荷不同而要求不同。对于高轴荷车，因为侧倾刚度要求较高，带来扭转刚度和弹簧刚度要求较大。扭转刚度增大的方法从扭梁结构方面，主要包括形状和尺寸变量，变量提升都会带来质量及成本的提升。因此，满足轻量化要求的扭转梁后桥需要具备在质量较轻的同时具备较大的扭转刚度。
 

1 扭转梁截面参数化模型建立
 

由扭转梁刚度公式可得到关键因子为外阔尺寸、尺寸变量及形状变量。

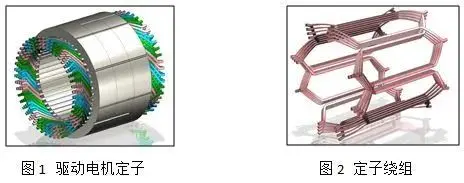
如图1所示闭口梁参数化模型，可实现形状一定范围内快速变化。

图1 参数化模型

Fig.1 Parametric model 

如图2,3所示，开口梁参数化变量主要包括外阔尺寸、形状变量、尺寸变量。形状变量包括三个截面的高度和宽度，第二截面和第三截面的位置，以及开口方向（开口向下到开口向前连续变化），这些变量共同决定了横梁应力的趋势及刚度大小。尺寸变量包括横梁和纵臂厚度，横梁厚度直接影响扭梁刚度及耐久性能；而纵臂厚度直接影响滥用性能。

 

图2 截面选取定义

Fig.2 Section Selection Definition

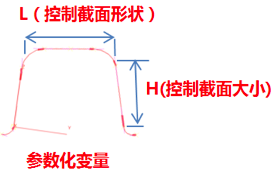
图3 截面参数化示意图

Fig.3 Section parametric diagram

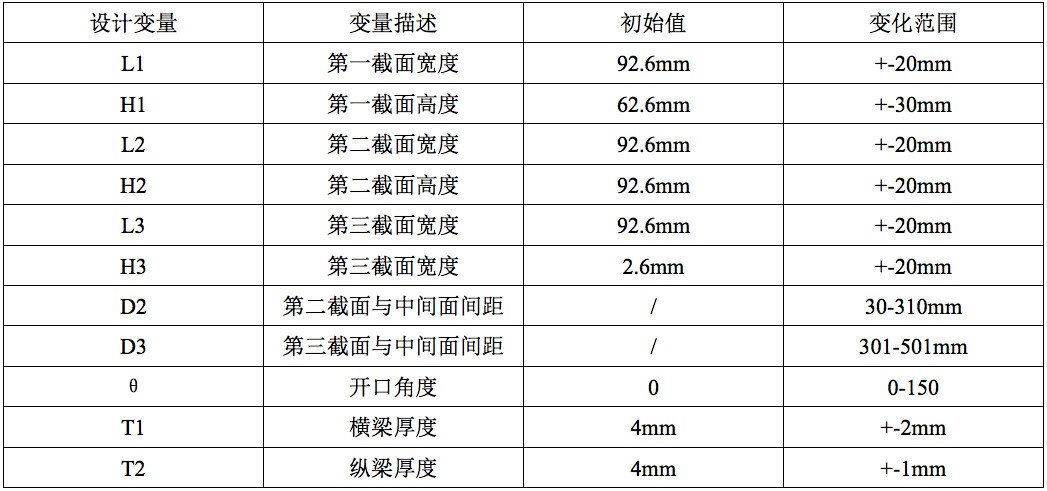
扭转梁参数化模型需覆盖车型的轮距范围，并满足现有车身连接点与轮心相对位置的要求。如表1，对轮距和纵臂长度实现范围选择。轮距范围为1400-1800mm。纵臂长度，范围为400-500mm。

表1 参数化变量取值范围

Table.1 Parametric value range

2 基于Isight设计流程

DOE设计方法选择优化超拉丁方方法。拉丁方试验设计将因素按水平竖排一个随机矩阵，即拉丁方矩阵，在同一列中任何因素的水平均无重复。如图4所示，优化拉丁方试验设计方法采用正交性较好的初始解，综合考虑拉丁方矩阵的正交性和均匀性。

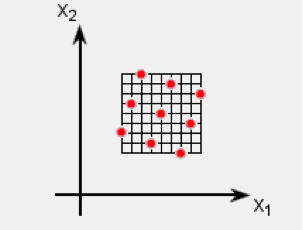
图4 优化超拉丁方方法选点方法

Fig.4 Optimal Latin Hypercube sampling method

分别对9个形状变量及2个尺寸变量按照优化超拉丁采样试验，共1000个试验以求得最优解。优化工况为刚度要、耐久、滥用变形性能要求，优化目标为质量最小。优化方法如下：

图5 自动化优化流程

Fig.5 Automatic optimization flow

3 扭转梁优化最优结构

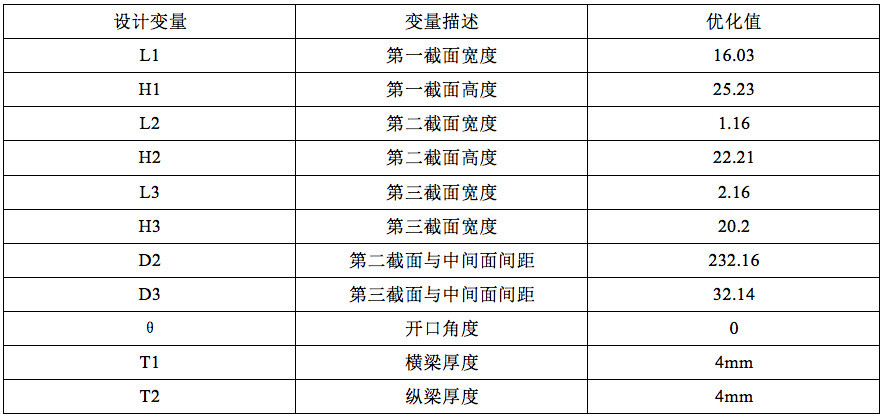
通过DOE优化，得到了形状和尺寸变量最优解，其结果如表2所示：

表2 参数最优解

Table.2 Parametric optimized value

如图6中原结构与优化结构对比图所示，红色部分为优化结构，蓝色部分为原结构，可以发现优化的结构横梁两端抬高，更强的抗扭能力有效降低横梁应力，耐久性能更优。相较于传统的扭转梁优化设计流程，设计周期从3周减少为2天，缩短了90%的优化周期，极大地提升了扭转梁设计的周期与效率。

图6 优化结构对比图

Fig.6 base and optimized structure diagram

4 最优参数性能验证

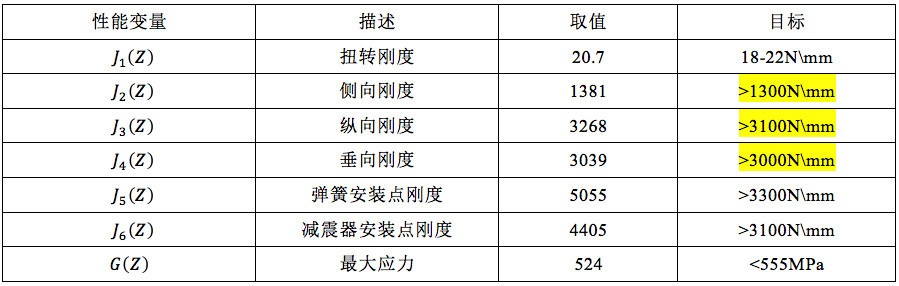
扭转梁性能要求主要包括操稳及耐久性能。其中操稳对扭转梁结构件的要求可以分解到刚度要求上，刚度主要包括扭转刚度、纵向刚度、侧向刚度、垂向刚度、弹簧安装点刚度、减震器安装点刚度。而扭梁扭转刚度和弹簧刚度决定了扭转梁后悬架的侧倾刚度，侧向刚度决定了后悬架的横向刚度。

从表3中性能结果表可见，包括扭转刚度、侧向刚度、垂向刚度、弹簧安装点刚度、减震器安装点刚度全部满足目标值。

表3 性能结果表

Table.3 Function result

优化方案的试制样件，经过台架考核后，可以看到试验结果均满足20万次的目标值，如表4和图7所示。因此，该优化方案可以同时满足低频扭转耐久寿命要求。

表4 台架试验结果

Table.3 Rig-test result

图7 台架验证

Fig.7 Rig-test validation

综上所述，基于Isight的参数化设计而得的汽车扭转梁优化结构，其操稳及耐久性能都得到优化的同时，轻量化意义也得到了进一步提升。

5 结论

（1）基于Isight的参数化设计方法优化得到的扭转梁，经过台架验证，发现扭转刚度、侧向刚度、垂向刚度、弹簧安装点刚度、减震器安装点刚度，以及耐久性能全部满足要求，同时方案具备较好的轻量化意义。

（2）基于Isight的汽车扭转梁参数化设计方法，相较于传统的扭转梁优化设计流程，缩短了90%的优化周期，极大地提升了扭转梁设计的周期与效率。

参考文献

[1] 宋凯,段利斌,陈涛,陈艾国.全参数化概念车身协同开发与快速化结构设计研究[J].中国机械工程,2014,3(25):6

Song Kai, Duan Libin, Chen Tao, Chen Aiguo. Collaborative Development and Rapid Structure Design based on Full Parametric Concept Car Body[J].China Mechanical Engineering,2014,3(25):6

[2] 王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,1(47):2

Wang Ping, Zheng Songlin,Wu Guangqiang. Multidisciplinary Design Optimization of Vehicle Body Structure based on.Collaborative Optimization and Multi-objective Genetic Algorithm[J]. Journalof China Mechanical Engineering,2011,1(47):2

[3] 李锦,苏小平,王宏楠,陈宇晖,张才伟.基于灵敏度分析的轿车副车架轻量化研究[J].机械科学与技术,2013,11(32):11 

Li Jin，Su Xiaoping，Wang Hongnan，Chen Yuhui，Zhang Caiwei.Study on the Lightweight of Car Subframe based on the Sentivity Analysis Method[J].Mechanical Science and Technology for Aerospace Engineering,2013,11(32):11

[4] 蒋荣超,王登峰,秦民,蒋永峰.基于疲劳寿命的轿车后悬架扭转梁轻量化设计[J].吉林大学学报（工学版）,2016,1(46):1

Jiang Rongchao, Wang Dengfeng, Qing Ming, Jiang Yongfeng.Lightweight design of twist beam of rear suspension of passenger carbased on fatigue life. Journal of Jilin University (Engineering and Technology Edition) [J],2016,1(46):1

[5] Georgios Papaioannou, Dimitrios Koulocheris. An approach for minimizing the number of objectivefunctions in the optimization of vehicle suspension systems. Journal of Soundand Vibration[J]. 2018,435:149-169

[6] 李剑如.扭转梁扭转刚度的理论计算方法研究[J]. 机械强度, 2015,2.215-225

Li jianru. Research on the method of torsion stiffness calculation in theory for twist beam [J]. Journal of Mechanical Strength, 2015, 2.215-225